[zurück] [physik] [home] [rgr] [mathematik] Regression
Was ist Regression ???
Der Begriff "Regression" (lat.) bedeutet soviel wie "Rückschritt" bzw. "Absinken auf frühere Entwicklungsstufe".
Jede Messung ist mit einem Fehler behaftet und so sind auch Messwerttabellen, in denen eine zu messende Größe y in Abhängigkeit von einer Größe x dargestellt wird grundsätzlich mit einem Fehler behaftet.
In der Praxis besteht zwischen den Größen x und y häufig ein funktionaler Zusammenhang.
z.B. - Zusammenhang von Kraft F und Längenänderung Ds einer Feder bei der
Untersuchung des Hookschen Gesetzes
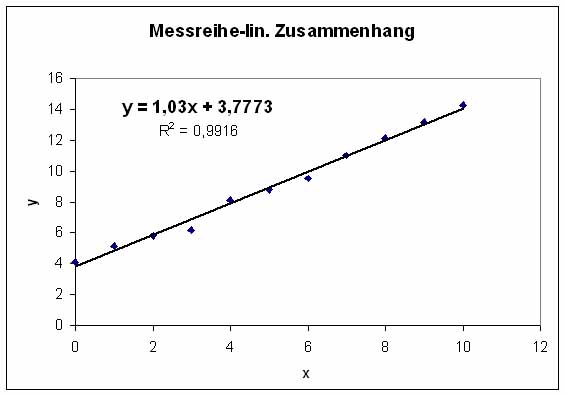
Der funktionale Zusammenhang ist hier linear, der Graph im Diagramm ist somit
eine Gerade und genügt der Form der Geradengleichung y=mx+b
- experimentelle Bestimmung der Halbwertszeit beim Zerfall des Bariumisotops
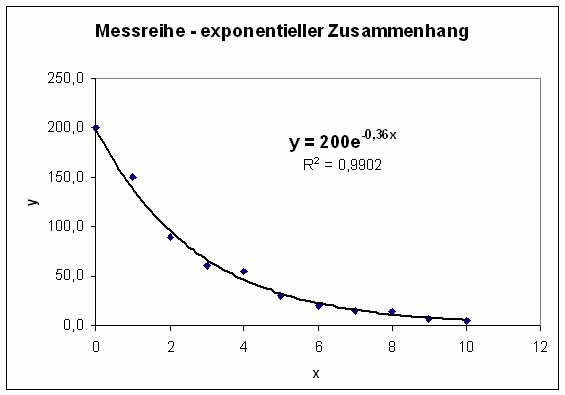
Der Zusammenhang zwischen Zählrate und Zeit genügt hier einer
Exponentialfunktion, also der Form y = A*eBx
Ziel der Regression ist es, die Koeffizienten A und B (bzw. m und b) des funktionalen Zusammenhangs zu bestimmen.
Daher musst du zunächst prüfen, in welchem Zusammenhang (linear, quadratisch, exponentiell, ...) deine Messwertpaare stehen. Danach kannst du mit der Regression beginnen.
Das eigentliche Regressionsverfahren erfordert einen großen Rechenaufwand, aber den können uns EXCEL und Taschenrechner wie der CASIO fx 991 abnehmen.
Ein Vorteil der Regression ist, dass zufällige Fehler weitgehend ausgeglichen werden, da der Graph der Regressionsfunktion "den Weg durch die Messwerte wählt", der die geringste Abweichung aufweist.
Solltest du Probleme mit der Vorstellung haben, so wähle diesen Link zu einem wirklich tollen JAVA Applet der UNI Münster an. Hier kannst du interaktiv die Veränderung der beschriebenen Parameter in Abhängigkeit von den gesetzten Punkten erleben.
Beide Graphen zeigen, dass sie "optimal" in die Punkte der Messwertpaare eingepasst wurden. Aus der Funktionsgleichung können die Koeffizienten A und B abgelesen werden.
Der Wert R2 unter der Funktionsgleichung ist das Bestimmtheitsmaß der Regression. Er gibt die "Qualität" der erhaltenen Funktion an. R2 nimmt dabei Werte von 0 bis 1 an. Das Bestimmtheitsmaß 1 steht hierbei für das Optimum und bedeutet, dass alle Messwertpaare auf dem Graphen liegen.
Regression mit EXCEL
Da viele Messwerttabellen bereits in EXCEL aufgenommen werden, bietet sich hier auch die Weiterarbeit an. Nachdem die Messwerte in einem Diagramm auch grafisch dargestellt wurden, musst du
mit der rechten Maustaste auf einen Messpunkt klicken. Es öffnet sich ein kleines Fenster, in dem du
die Option "Trendlinie hinzufügen ..." wählst.
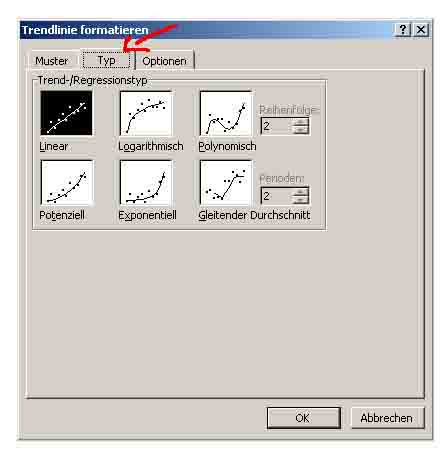
Im neuen Fenster "Trendlinie formatieren" wählst du die Art der gewünschten Regression (linear, logarithmisch, polynomisch, ...). Hierzu musst du wissen welcher funktionale Zusammenhang zwischen deinen Messwerten besteht. Bestätige deine Auswahl noch nicht mit OK.
Wahl des Regressionstyps
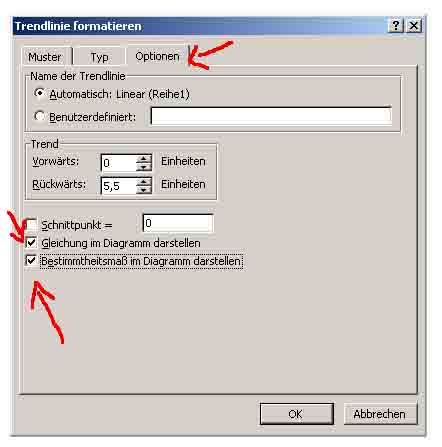
Anwahl von Gleichung und Bestimmtheitsmaß
Im Kopf des Fensters findest du die Registrierkarte "Option". Diese wählst du an und
setzt in die Felder "Gleichung im Diagramm darstellen" und "Bestimmtheitsmaß im Diagramm darstellen" einen Haken.
Ein Klick auf OK und du erhältst einen Graphen mit Ausgleichsgraph, funktionalem Zusammenhang und Bestimmtheitsmaß, wie oben dargestellt.
Regression mit dem Taschenrechner "CASIO-fx991..."
Im täglichen Unterricht steht leider nicht jedem Schüler ein PC zur Verfügung. Aber auch mit dem Taschenrechner ist die Berechnung der Regressionskoeffizienten schnell und einfach durchzuführen. Dazu wählst du
über die Taste MODE den Regressionsmodus (REG). Hier kannst du dich zwischen den verschiedenen Regressionsarten
Lin Log Exp Pwr Inv Qard linear logarithmisch exponentiell potentiell invers quadratisch wählen.
Die Eingabe der Werte erfolgt paarweise. x-Wert, y-Wert. Jedes Wertepaar wird mit der Taste DT (Doppelbelegung von M+) bestätigt. Für das Komma, mit dem du x- und y-Wert trennst ist nicht der Dezimalpunkt, sondern die "Kommataste" rechts neben der Klammer zu verwenden.
Sind alle Werte eingegeben, können die Regressionskoeffizienten abgerufen werden. Dazu betätigst du die Tasten SHIFT und 2. Jetzt kannst du aus dem Menü die Koeffizienten A und B sowie den Korrelationskoeffizienten r abrufen.
Bevor du eine weitere Regression beginnst, lösche unbedingt den Datenspeicher, da die eingegebenen Werte bis zu ihrer Löschung im Speicher verbleiben und bei einer neuen Berechnung diese selbstverständlich verfälschen. ( SHIFT CLR 1 )
- lineare Regression
interaktives JAWA - Applet zur linearen Regression von der Universität Münster klick hier !
http://medweb.uni-muenster.de/institute/imib/lehre/skripte/biomathe/bio/regap3.html
Korrelationskoeffizient / Bestimmtheitsmaß
- exponentielle Regression
- quadratische Regression
... in Arbeit ...