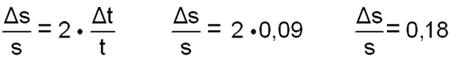| [zurück] | [physik] | [home] | [rgr] | [mathematik] |
- Fehlerfortpflanzung
Was ist das denn?
Bei der Fehlerfortpflanzung geht es darum, wie sich Messwerte verschiedener Größen auf das Endergebnis auswirken. Also am Beispiel - du misst den Weg s und die Zeit t um die Geschwindigkeit v eines Körpers zu bestimmen. Beide Größen, Weg s und Zeit t, sind als Messwerte mit einem Fehler behaftet und beeinflussen so deine berechnete Geschwindigkeit v.
Aber wie?
Wir gehen davon aus, dass deine Zeitmessung mit einem Fehler von 5% bzw. 0,05 und die Wegmessung mit einem Fehler von 3% bzw. 0,03 behaftet ist.
Allgemein ist die Betrachtung der Fehlerfortpflanzung nicht ganz einfach und erfordert mathematische Kenntnisse, die den Rahmen der Schule verlassen.
|
In den meisten Fällen kann die Fehlerfortpflanzung auf drei Spezialfälle reduziert werden, die schon mit Kenntnissen der Klasse 7 bearbeitet werden können. |
|
|
Also kein Grund zur Panik - halb so schlimm! |
|
| In der Regel können wir 3 Fälle unterscheiden: | |
| Die Messwerte gehen in die Rechnung ein, als | |
| a) | Gehen zwei fehlerbehaftete Größen a und b als Produkt (a*b) oder als Quotient (a/b) in eine Rechnung ein, so ist der relative Fehler des Produktes bzw. des Quotienten kleiner oder gleich der Summe der relativen Fehler. |
|
einfache Rechnung bis Klasse 9 |
 |
|||
| zum Beispiel von Oben: | |||
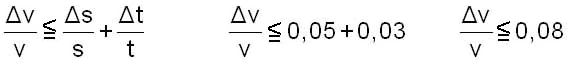 |
|||
| Die Berechnung der Geschwindigkeit ist mit einem Fehler von weniger als 8% behaftet. | |||
| Ihr könnt bereits mit Wurzeln rechnen und kennt den PYTHAGORAS - dann geht es auch genauer. |
 |
||
| Gehen zwei fehlerbehaftete Größen a und b als Produkt (a*b) oder als Quotient (a/b) in eine Rechnung ein, so ist der relative Fehler des Produktes bzw. des Quotienten gleich der Wurzel, aus den Quadraten der relativen Fehler. | |||
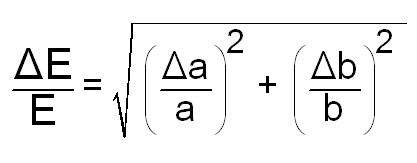 |
|||
|
|
|||
| Die Berechnung der Geschwindigkeit ist mit einem Fehler von 5,8% behaftet. | |||
| Warum die Wurzel der Quadrate? Das soll die folgende Grafik erklären. | |||
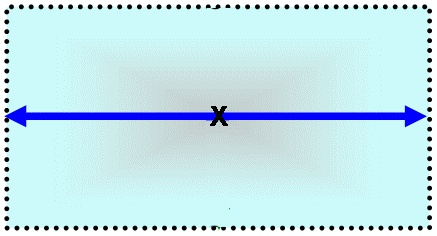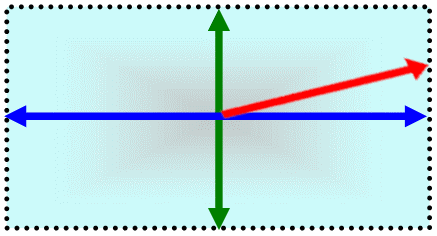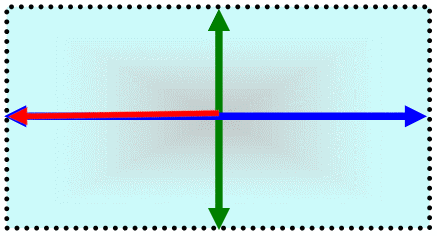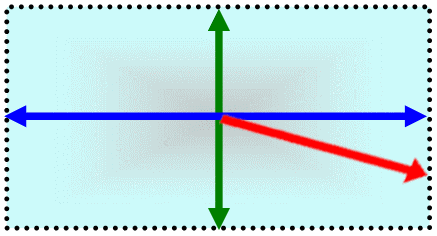 |
Der Fehler
der Größe a wird hier um den "wahre" Wert abgetragen
(Fehlerbalken). Gleiches passiert auch mit dem
Fehler von Wert von b. Der berechnete Wert, das Produkt, befindet sich also im dargestellten Rechteck. Die größtmögliche Abweichung stellt die Diagonale im Rechteck dar.
|
||
| b) | Geht eine fehlerbehaftete Größe a in der n-ten Potenz in eine Rechnung ein, so ist der relative Fehler der; Potenz gleich das n-fache des relativen Fehlers. | |
|
Beispiel: Welchen Weg hat ein Körper im freien Fall nach
der Zeit t zurückgelegt? g ist als Ortsfaktor eine gegebene Konstante und somit frei von Messfehlern. Die Zeit t wurde mit der Stoppuhr gemessen und habe einen Fehler von 9% bzw. 0,09.
Die Berechnung des Fallweges ist mit einem Fehler von 18% bzw. 0,18 behaftet. |
|
|
| c) |
Der Fehler einer Summe wird aus der Summe der absoluten
Fehler berechnet.
Beispiel: Es werden zwei Längen gemessen l1 = 0,25m; und l2 = 0,30m. Die Ungenauigkeit bei der Ablesung betrage 5mm bzw. 0,005m. Fehler am Maßband bleiben hier unberücksichtigt. Werden die Größen l1 und l2 addiert, so erhalten wir lges = l1 + l2 = 0,55m.
Die Summe der Absoluten Fehler beträgt 5mm +5mm = 10mm = 0,01m Der Relative Fehler beträgt 0,01m/0,55m = 0,018 bzw. 1,8% |
|