Fehlerbalken

Messwertaufnahme - Messfehler

Alle Messwerte (außer einer Zählung) sind mit einem Fehler behaftet. Fehler sind hier aber nichts Negatives, sie gehören zum Messprozess. Um Aussagen zu physikalischen Gesetzmäßigkeiten treffen zu können, musst du aber wissen, wie groß dein Fehler ist, bzw. wie gut deine Messwerte sind. Weiter kannst du abschätzen, ob du ggf. deine Messung verbessern musst, oder ob das auf das Endergebnis keinen großen Einfluss hat.

z.B. Du misst die Zeit mit einer Handstoppuhr, die auf 1/10 s genau misst. Ist es sinnvoll, eine Stoppuhr zu verwenden, die auf 1/100 s genau misst?

Diese Frage kannst du mit folgendem Experiment schnell beantworten.

Viele Schüler bekommen eine Stoppuhr oder nutzen ihr Handy, den iPod oder Ähnliches. Einer sagt Start und alle starten ihre Stoppuhr. Nach einer Weile heißt es Stopp. Notiere die Zeiten in einer Tabelle.

In nebenstehender Tabelle siehst du Messwerte zwischen 9,32 s und 10,12 s. Zwischen dem größten und dem kleinsten Wert liegen also 0,9 s. Der Mittelwert der Zeitmessungen beträgt 9,536 s. Die Abweichungen vom Mittelwert liegt zwischen -3,3 % und +6,1 %.

Nr.	Zeit in s	Abweichung zum Mittelwert
1	9,5	-0,4 %
2	9,32	-2,3 %
3	10,12	+6,1 %
4	9,52	-0,17 %
5	9,22	-3,3 %
Mittel-wert	9,536

Wie sinnvoll ist es also auf 1/100 s genau zu messen???

Die Reaktionszeit liegt allgemein bei ca. 0,5 s . Das bestätigen auch die Messwerte. Für kürzere Messintervalle wird bei gleicher Reaktionszeit der relative Fehler, also der Fehler in Prozent, größer. Demnach ist es sinnlos, auf 1/100 s genau zu messen. Besser wäre es hier den Messprozess zu optimieren und die Reaktionszeit zu verkürzen. Aber wie?

Fehlerbalken

Ein Spielzeugauto mit Elektromotor fährt über eine Strecke von 8 m, dabei wurde alle 2 m die Zeit gestoppt.

t / s	s / m
0	0
1,2	2
1,8	4
2,8	6
4,3	8

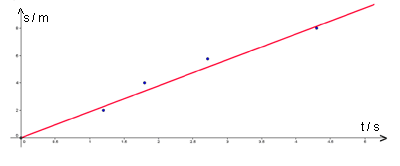Es ist schnell zu erkennen, dass die Werte nicht auf einer Ursprungsgerade liegen. Aber die Bewegung war doch gleichförmig!?

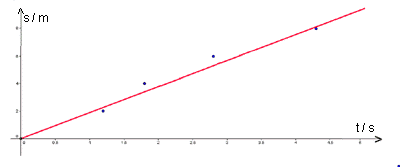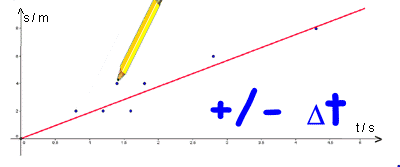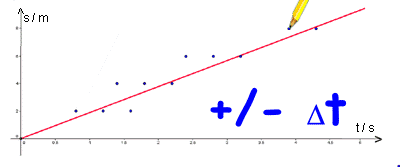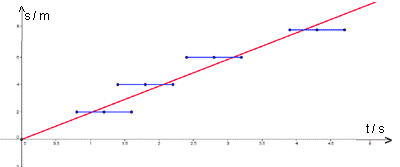Den Messfehler bei der Wegmessung s wollen wir zunächst vernachlässigen. Dann kannst du die Messwerte wie im Diagramm dargestellt abtragen. Da die Zeitmessung mit einem Fehler behaftet ist, stellen wir diese auch nicht als Punkt sondern mit einem Balken dar.

Die Balken berücksichtigen den Fehler (das Fehlerintervall) der Zeitmessung. Es ist zu erkennen, dass durch die Balken jetzt eine Gerade gelegt werden kann. Die Bewegung ist gleichförmig.

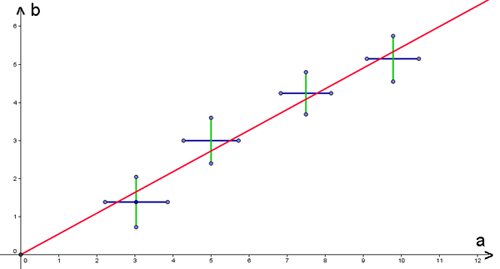
Im oben betrachteten Beispiel sind wir davon ausgegangen, dass nur die Zeitmessung mit einem Fehler behaftet war. Das ist i.d.R. bei diesem Beispiel auch ausreichend. Ist hingegen auch der Fehler der zweiten Größe zu berücksichtigen, dann spannen die Fehlerintervalle beider Messwerte eine Fläche auf.

In der Berechnung könnt ihr dann die Gesetzmäßigkeiten der Fehlerfortpflanzung nutzen.

zur Fehlerfortpflanzung