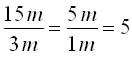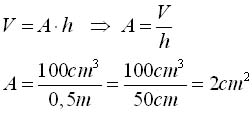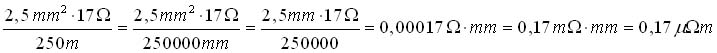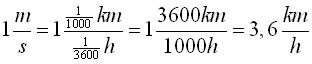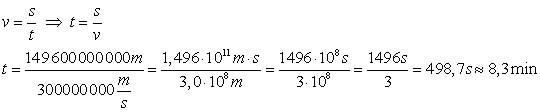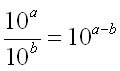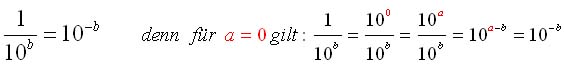Zehnerpotenzen / Einheitenvorsätze

 
Jede physikalische Größe besteht aus Zahlwert und Einheit. Bei einigen physikalischen Größen wie Kraft, Druck, Geschwindigkeit,... ist auch die Richtung der Größe von Interesse. Diese Größen heißen vektorielle Größen, doch dazu später.

Häufig ist es nicht sinnvoll, eine Größe in ihrer Grundform ( ohne Einheitenvorsatz )  anzugeben z.B.

- die Länge einer Büroklammer ( 0,032m)

- die Strecke von Rotenburg /W nach  München (739900 m)

- die Stärke einer Plastikfolie ( 0,00001m)

- die Ladung eines Elektrons (0,000 000 000 000 000 000 160 217 646 2 C )

 

Um diese Größen übersichtlich angeben zu können und sich nicht ausschließlich auf das Zählen der Nullen zu konzentrieren, bieten sich zwei einfache Möglichkeiten an.

 

1. Versehen der Einheiten mit Vorsatz

2. Angabe in Zehnerpotenzen

 

 

           

Vorsatz gesprochen

Bedeutung

 Zehnerpotenz
y Yocto 1/1 000 000 000 000 000 000 000 000   10-24
z Zepto 1/1 000 000 000 000 000 000 000 ein Trilliardstel 10-21
a Atto 1/1 000 000 000 000 000 000 ein Trillionstel 10-18
f Femto 1/1 000 000 000 000 000 ein Billiardstel 10-15
p Piko 1/1 000 000 000 000 ein Billionstel 10-12
n Nano 1/1 000 000 000 ein Milliardstel 10-9
µ Mikro 1/1 000 000 = 0,000 001 ein Millionstel 10-6
m Milli 1/1000 = 0,001 ein Tausendstel 10-3
c Zenti 1/100 = 0,01 ein Hundertstel 10-2
d Dezi

1/10 = 0,1

ein Zehntel 10-1
da Deka 10 Zehn 101 = 10
h Hekto 100 Hundert 102 = 100
k Kilo 1 000 Tausend 103 = 1000
M Mega 1 000 000 Million 106
G Giga 1 000 000 000 Milliarde 109
T Tera 1 000 000 000 000 Billion 1012
P Peta 1 000 000 000 000 000 Billiarde 1015
E Exa 1 000 000 000 000 000 000 Trillion 1018
Z Zetta 1 000 000 000 000 000 000 000 Trilliarde 1021
Y Yotta 1 000 000 000 000 000 000 000 000   1024

 

Die kursiv geschriebenen Vorsätze haben nur in wenigen Bereichen eine Bedeutung. In der Schulphysik werden sie keine Anwendung finden.

 

Bei der Verwendung von Einheitenvorsätzen sind einige Regeln zu beachten:

 

  1. Keine Einheit darf mit mehreren Vorzeichen versehen werden.  ( z.B. 5 000 000 Hz = 5 kkHz falsch;  5000000 Hz  = 5 MHz richtig )

  2. Die Einheit von Ergebnissen sollte mit einem Vorsatz versehen werden, der den Zahlwert in einen Bereich  zwischen 0,1 und 1000 bringt.

  3. Die Kombination von Einheit und Vorsatz gilt als ein Symbol, so dass auch Potenzen für den Vorsatz gelten.

 

          

z.B.      1km    =  

1000 m

 1km2  =  

1km * 1km             = 1000m * 1000m              = 1 000 000 m2

1cm3  =  

1cm * 1cm * 1cm  = 0,01m * 0,01m * 0,01m  = 0,000 001m3

 

 

In vielen Rechnungen ist es sinnvoll, Einheiten vor dem Weiterrechnen zu kürzen.

                    

 

 

Hierbei müsst ihr beachten, dass nur gleiche Einheiten gegeneinander gekürzt werden können. Es kommt  jedoch nicht nur auf die physikalische Größe, sondern auch auf den Einheitenvorsatz an.

 

Ein Quader habe das Volumen V = 100cm2. Welche Grundfläche hat der Quader, wenn seine Höhe 0,5m beträgt?

 

Die Höhe 0,5m wird in 50cm umgerechnet. Die Einheit cm kann dann gegen die cm3 aus dem Zähler gekürzt werden.

 

 
Die Einheitenvorsätze von Widerstand [R] = Ω und Länge [s] = m können auch zusammengefasst werden.

 

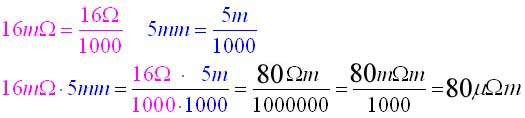Das gilt selbstverständlich auch bei der Division,

z.B.

 

aber auch für Umrechnungen.

 

 
Noch komplizierter wird es, wenn auch die umzurechnenden Größen mit einem Exponenten versehen sind, (z.B. 2,6 µm2  in ....m2 ) oder einzelne Größen sehr groß ( Abstand Erde – Sonne ) oder sehr klein werden. ( Masse einen Elektrons )

 

Dann ist es einfacher mit Zehnerpotenzen zu arbeiten. Das Einfache daran ist, dass auch die Zehnerpotenzen gekürzt werden können.

 

Beispiel 1: Wie viel Zeit benötigt ein Signal bzw. "ein Lichtstrahl" von der Sonne zur Erde. Die mittlere Entfernung Erde Sonne beträgt 149 600 000 km = 149 600 000 000 m  und das Licht breitet sich mit einer konstanten Geschwindigkeit von 300 000km/s aus.

 

Ein Signal von der Sonne benötigt als rund 8 min und 18 s um die Erde zu erreichen.

 

Beispiel 2 - Einheit mit Potenz

Bei einer Explosion wird ein Teilchen mit  a =  1 km/s2   für t = 10ms beschleunigt. Welchen Weg hat es während der Beschleunigung  zurückgelegt?

 

Das Teilchen hat in den 10ms einen Weg von 5cm zurückgelegt.

Beispiel 3 - Einheiten mit Potenzen - Kürzen von Zehnerpotenzen

Auf eine Platte der Fläche  A = 80cm2 wirkt ein Druck von  p = 100 kPa. Wie Groß ist die Kraft, die der Druck verursacht?

Einheit des Drucks p: 
 
1 kPa = 1000 Pa = 1*10*10*10 Pa = 1*103 Pa
(10-2)2 = 10-2 * 10-2 = 10-2+(-2) = 10-4
   
100*103 = 100*10*10*10 = 100 000 = 105

Die Einheiten der Flächen (m2) in Zähler und Nenner werden gekürzt.
   

       F = 800 N

   
   

allgemein gilt:

Multiplikation von Potenzen mit gleicher Basis:

Die Exponenten werden addiert, die Basen bleiben erhalten.

Division von Potenzen mit gleicher Basis:

Die Exponenten werden subtrahiert, die Basen bleiben erhalten.

   

 

Bei der Rechnung mit Zehnerpotenzen kann also auf Einheitenvorsätze weitgehend verzichtet werden. Ferner bleiben die zu betrachtenden Zahlen übersichtlich und nach etwas Übung können viele Ergebnisse durch vorheriges Kürzen bereits abgeschätzt werden (Überschlag).
Ihr erspart euch also, wiederholt Vor- und Nachkommastellen auszuzählen, was nicht nur sehr langweilig ist, sondern bei den "Nichtganzsoschönschreibern" auch schnell zu Fehlern führen kann.

    weiter   ... in Arbeit ....

[home] [wegweiser] [physik] [mathematik]
U. Konrad [Kontakt] [them. Übersicht] [Videos] [alphab. Übersicht] [intern]