| Der Massendefekt |
 |
|
|
" 1 + 1 + 1 + 1 > 4 " ! ?
Diese Ungleichung sieht zunächst sehr befremdlich aus, kennzeichnet jedoch, wie auch die nebenstehende Abbildung den Massendefekt. Die Summe der Einzelmassen der Kernbausteine ist größer als die Masse des Kerns.
|
||
Gleichnamige Ladungen
stoßen einander ab. Warum können dann 2 Protonen auf so engem
Raum in einem Kern vereinigt werden? Die Neutronen sind
elektrisch neutral, haben also bzgl. der elektrostatischen Abstoßung
keinen Einfluss. In Experimenten zur Elektrostatik hast du
festgestellt, dass sich gleichnamige Ladungen abstoßen.
dass heißt, je kleiner der Abstand der Ladungen, desto größer die abstoßende Kraft. Im Kern haben die Protonen einen unvorstellbar kleinen Abstand. Hier wirken weitere Kräfte, die bisher nicht besprochen wurden - die KRENKRÄFTE. KERNKRÄFTE sind stärker als die Kräfte der elektrostatischen Abstoßung, haben aber nur eine sehr kleine Reichweite. Aus obiger Gleichung und der Abbildung de Balkenwaage erkennst du, dass die Masse des Kerns kleiner ist, als die seiner Bestandteile. Diese Differenz Dm ist der Massendefekt. |
||
|
|
|
|
| Die Masse der Kernbausteine (Z-Anzahl der Protonen und N-Anzahl der Neutronen) ist größer als die Masse des Kerns |
|
Am Beispiel eines Helium - Kerns (Alpha-Teilchens) soll das an folgender Rechnung verdeutlicht werden. |
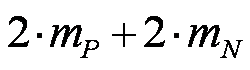 |
mP = 1,672635 * 10-27
kg mN = 1,67494 * 10-27 kg |
|
| 2*1,672635*10-27 kg + 2*1,67494*10-27 kg = 6,69515*10-27 kg |
|
|
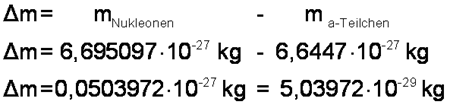 |
Beim α-Teilchen beträgt der Massendefekt ca. 5,04 * 10-29 kg. | |
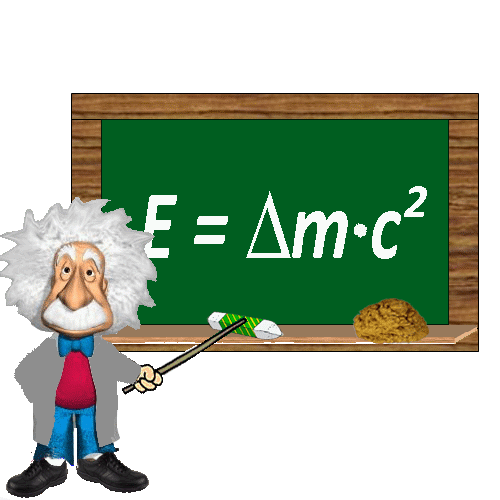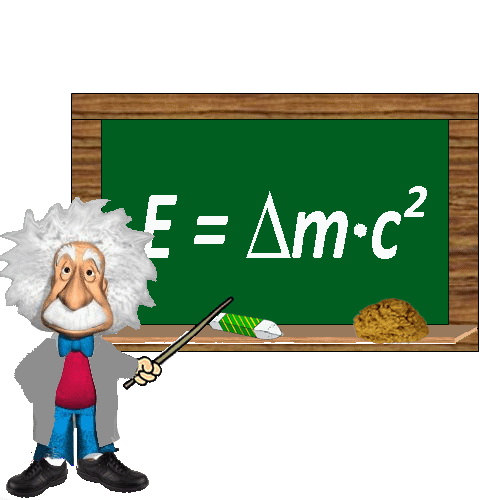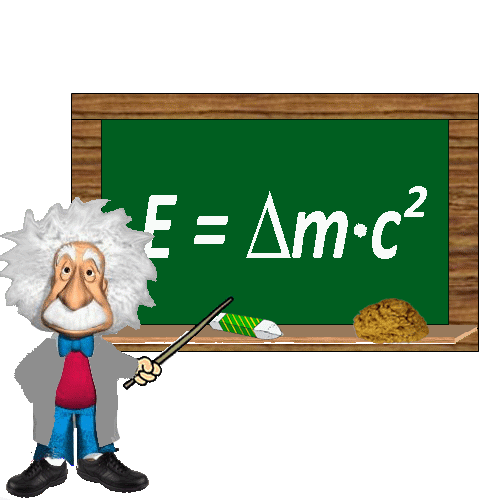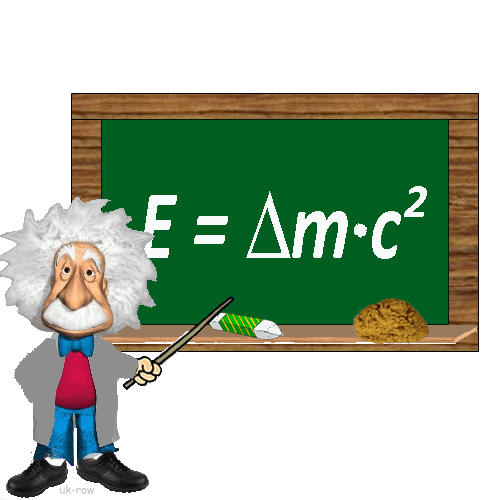 |
||
| Wo bleibt die Masse??? | ||
| Die Massendifferenz Dm steckt in der Bindungsenergie. Bei der Verbindung von 2 Protonen und 2 Neutronen zu einem He-Kern, wird die Bindungsenergie E=Dm*c2 frei. | ||
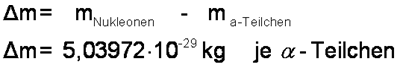 |
||
 |
E
– Energie
Dm – Masse
c
- Lichtgeschw. (c = 300.000 km/s)
|
|
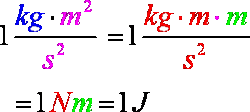 Einheitenbetrachtung Einheitenbetrachtung |
||
Bindungsenergie pro Heliumkern
|
||
Welche
Bindungsenergie steckt in 1 kg Helium?
|
||
| Ein He-Atom hat die Masse m = 6,6464725 * 10-27 kg |
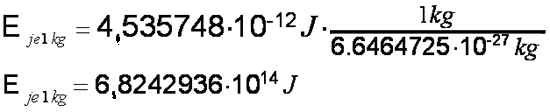 |
|
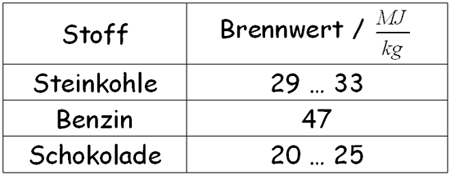 |
Vergleiche mit
den Brennwerten bekannter Brenn- und Treibstoffe
Bei der Verbrennung von 1 kg Steinkohle wird eine Energie von ca. 30 MJ in Wärmeenergie umgewandelt. Bei der Fusion von 2 Protonen und 2 Neutronen zu 1 kg Helium wird eine Energie frei, die um 7 Zehnerpotenzen, bzw. 10 Mio. mal größer ist. |
|
|
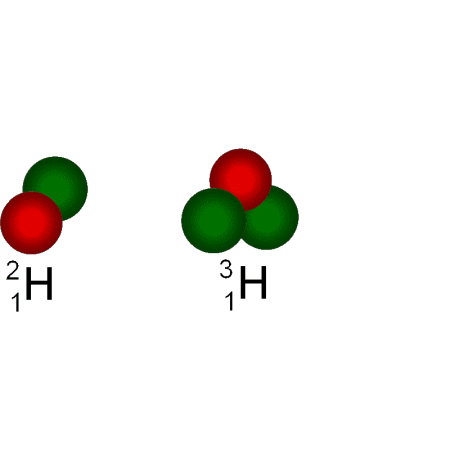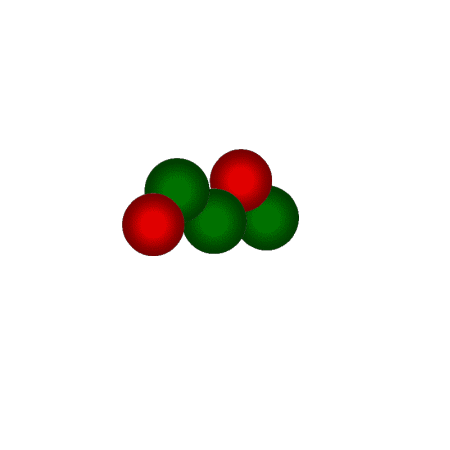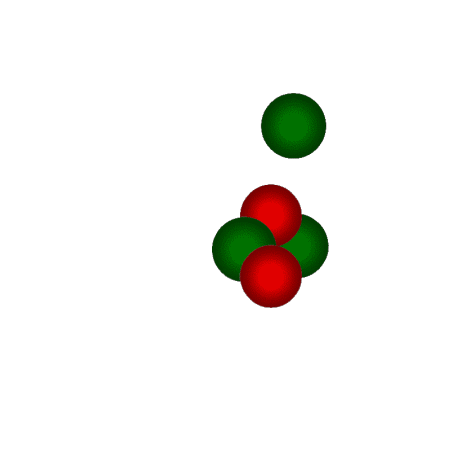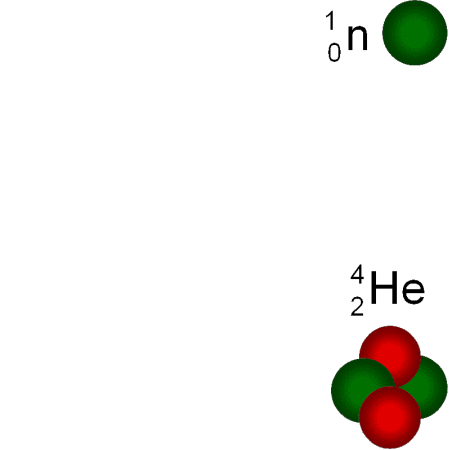
Die berechnete Energie ist aber nur ein theoretischer Wert. In der Praxis verbinden sich nicht 2 Protonen und 2 Neutronen, sondern Deuterium (H-2) und/oder Tritium (H-3). Die dabei frei werdende Energie ist etwas geringer. |
 |
|
| zur Kernspaltung | ||

