[zurück] [physik] [home] [rgr]   [mathematik]

Physik 5/6 - Optik

  • Linsen
  
An der Grenzschicht zweier optischer Medien ändert das Licht seine Ausbreitungsrichtung. (Bedingung α ungleich 0°)
Anders, als bei dem Glasquader im oberen Bild, hat die Kugel eine nich ebene Oberfläche. Das einfallende Licht trifft an jeder Stelle in einem anderen Winkel auf die Oberfläche der Kugel. Es wird an jeder Stelle in einem anderen Winkel gebrochen.

   

Lichtdurchlässige Körper mit einer gekrümmten Oberfläche bezeichnen wir als Linsen. Dabei unterscheiden wir zwischen den Grundformen:
  • Konvexlinse bzw. Sammellinse
  • Konkavlinse bzw Zerstreuungslinse

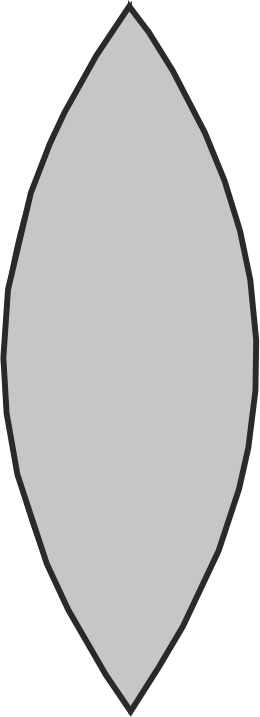
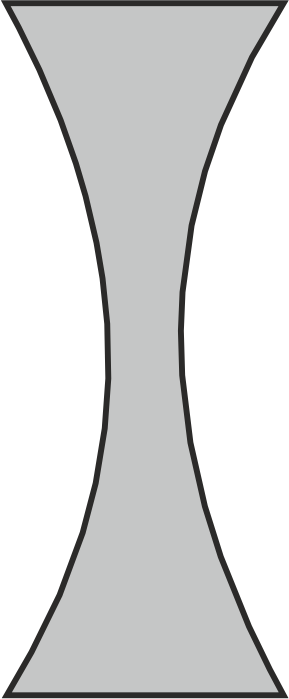
Konvex- bzw. Sammellinsen bündeln das einfallende Licht.

Konkav- bzw. Zerstreuungslinsen brechen das Licht so, dass die einfallenden Strahlen hinter der Linse weiter auseinanderlaufen.

 
Konvexlinse Konkavlinse  
Das folgende Foto zeigt die Kombination zweier Linsen. Während die, von der Lampe ausgehenden Lichtstrahlen, nach der Konkavlinse auseinanderlaufen, werden sie nach der Konvexlinse wieder gebündelt.

Am Bild erkennen wir, dass das Licht beim Übergang von der Luft zum Glas gebrochen wird. Beim Verlassen der Linse wird das Licht erneut gebrochen.

 
 

 

  • sphärische Linsen:

Sphärische Linsen sind die einfachsten Linsen. Die Oberfläche dieser Linsen ist Ausschnitt einer Kugel. In der Konstruktion in der Ebene können wir also auf einen Kreis reduzieren. An der Grafik ist zu erkennen, dass die Ränder der Linse als Ausschnitt der Kreise entstehen.

M ist dabei der Mittelpunkt des jeweiligen Kreises.

Wie schon am Hohlspiegel, so gibt es auch bei der Konvexlinse einen Brennpunkt F. Dieser liegt auf der halben Strecke des Radius zur Mittellinie der Linse. Den Abstand des Brennpunktes zur Linse bezeichnen wir als Brennweite f.

r = 2 f

 
weitere Linsenformen:https://de.wikipedia.org/wiki/Datei:Linsenarten.svg