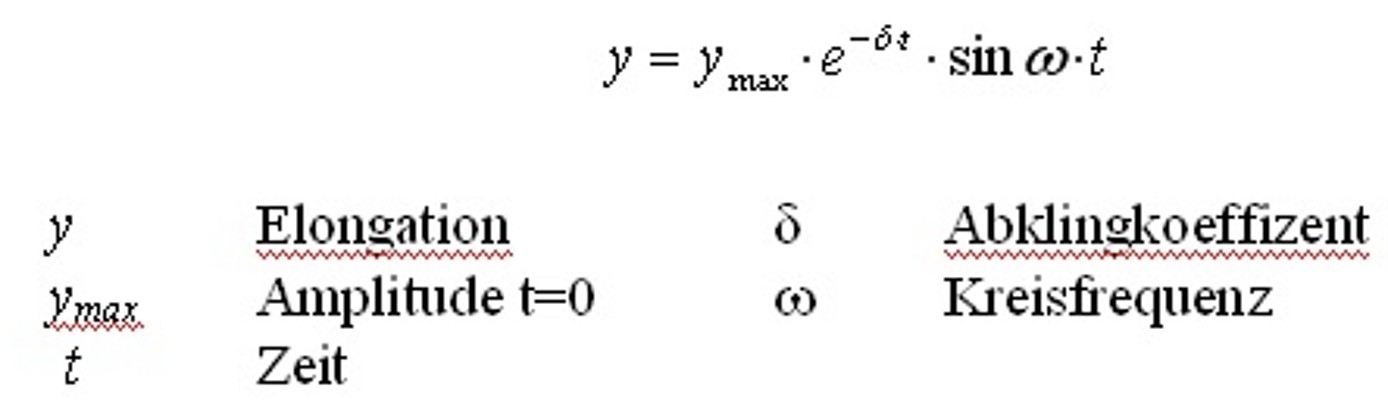Thema:

Aufnahme einer Schwingung zur Untersuchung des Dämpfungsverhaltens mithilfe einer Schattenprojektion

Versuchsidee:

In der Vorbetrachtung zu diesem Experiment wurde die Hypothese aufgestellt, dass die Abnahme der Amplituden einer Schwingung einer exponentiellen Form genügt. Die Annahme einer linearen Abnahme wurde aus theoretischen Gründen verworfen.

In dem vorliegenden Fall wird die Schwingung eines bifilar aufgehängten Fadenpendels mithilfe einer Schattenprojektion aufgenommen und das Dämpfungsverhalten dieser Schwingung untersucht.

Material:

- Oberlichtprojektor

- Pendelkörper (Stahlkugel mit Öse m = 300g)

- Faden (ca. 1,0m)

- Stativ

- weißes Papier (ca. 0,7m * 0,3m)

- Stift und Lineal

- Stopuhr

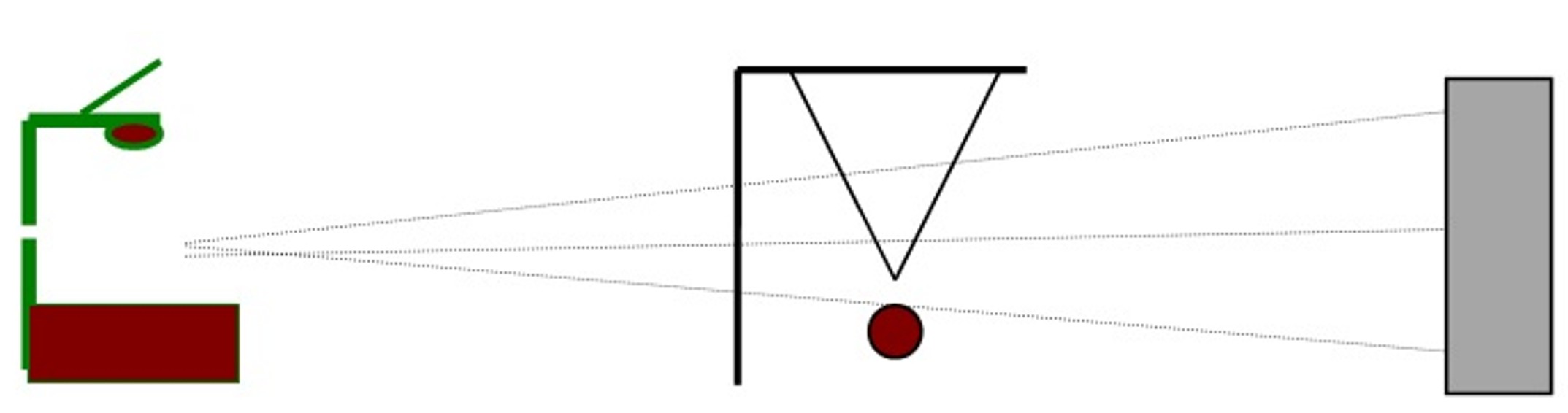
Versuchsskizze:

Oberlichtprojektor

Projektionswand

Stativ + Pendel

Äußere Beschreibung:

Versuchsaufbau:

Der Faden des Pendelkörpers wird bifilar am Stativ aufgehängt und vom Oberlichtprojektor bestrahlt. Die Projektionswand wird mit weißem Papier, auf dem eine Messskala gezeichnet ist, beklebt.

Durchführung:

Der Pendelkörper wird vom Projektor bestrahlt und es entsteht ein Schatten des Pendelkörpers auf der Projektionswand. Nun wird das Pendel um etwa 30° ausgelenkt und auf Befehl des Zeitmessers losgelassen. Ein Mitarbeiter guckt, wann die äußere Schattenseite des Pendelkörpers den Auslenkungspunkt a (z.B. 20cm) gerade noch berührt und gibt die Zeit, welche vom zweiten Mitarbeiter aufgeschrieben wird, bekannt. Dieses wird an verschiedenen Auslenkungspunkten (z.B. 19, 18, ..., 10cm usw.) wiederholt.

Messreihe:

Auslenkung	Zeit in sec
in cm	Versuch 1	Versuch 2	Versuch 3	Mittelwert
28	0	0	0	0
27	25	15		20,0
26	56	45	46	49,0
25	80	66		73,0
24	114	105	114	111,0
23	148	130		139,0
22	180	161	180	173,7
21	220	205		212,5
20	260	261	261	260,7
19	306	282		294,0
18	350	335	366	350,3
17	410	395		402,5

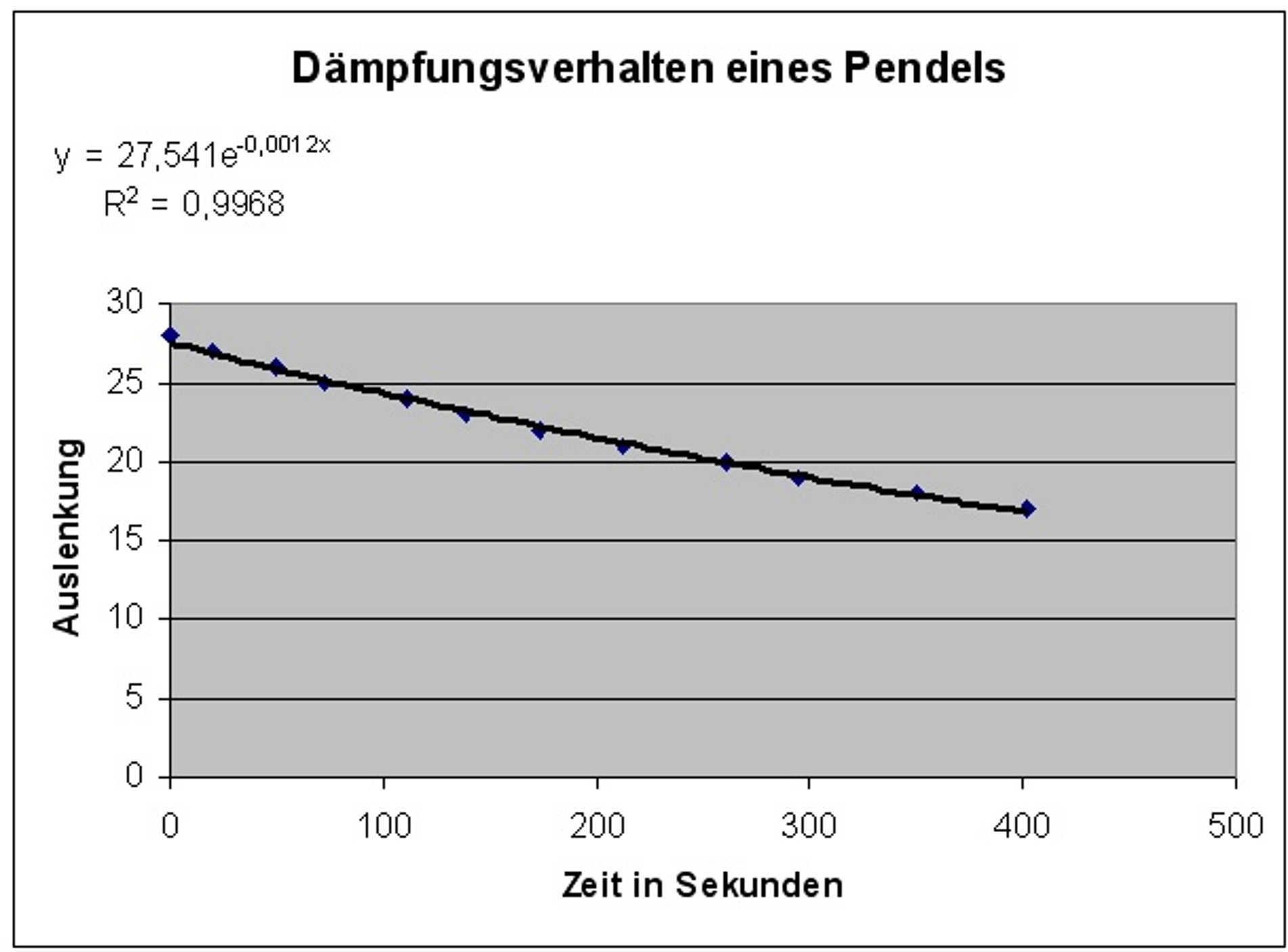
Die Auslenkung in cm ist hier nur ein relativer Wert. Durch die Schattenprojektion wird die Auslenkung in einem unbekannten Maßstab verzerrt. Deshalb kann im Graphen nicht die tatsächliche Auslenkung sondern nur das Verhältnis zwischen Auslenkung und Zeit dargestellt werden.

Fehlerrechnung / Fehleranalyse

Ablesefehler:

Beim Ablesen der aufgenommenen Daten ist von einem nicht unerheblichen Ablesefehler auszugehen. Durch die Schattenprojektion mit einer relativ großen Lichtquelle wirft die Kugel einen Kern- und einen Halbschatten. Wir haben versucht die Zeit zu bestimmen, in der der Kernschatten nicht mehr auf einem Skalapunkt zu sehen war. Durch die ständige Bewegung war es zum Teil ziemlich schwer den Kern vom Halbschatten zu unterscheiden. Dadurch kamen die Zeitstopbefehle oft zu früh oder zu spät.
Man muss hierbei bedenken, dass ein Zeitstopbefehl nur am Ende einer Periode Sinn machte. Die Auslenkungsabnahme innerhalb einer Periode konnte also nicht bestimmt werden. Es liegt in den Messungen der Zeit also ein maximaler Fehler von einer Periode vor (ca. 1-2 sek.) wenn man davon ausgeht, dass derjenige mit der Uhr perfekt gestoppt und derjenige an der Skala richtig geguckt hat. Davon kann man leider nicht ausgehen, es kommt also noch die Rektions-Zeit des Stoppers (ca. 1 sek.) und die „Verplantheit“ des Ablesers hinzu. Also im Falle eines Stoppbefehls, der schon am letzten oder erst am nächsten maximalen Ausschlag erfolgt haben sollte, ein Verfälschung des Ergebnisses um weitere 1-2 Sekunden.

Äußere Fehlereinflüsse:

Äußere Fehlereinflüsse sind bis auf 2 Dinge zu vernachlässigen.
1. Das Stativ, an dem das Pendel bifilar aufgehängt war, war nicht perfekt fixiert, es bewegte sich im Takt des Pendels ein wenig mit. Da das Stativ sich aber ähnlich wie der Pendel bewegte ist hierbei von einer Proportionalität auszugehen. Der verfälschende Proportionalitätsfaktor
müsste durch den unbekannten Verzerrungsfaktor durch die Schattenprojektion zu vernachlässigen sein. Trotzdem ist davon auszugehen, dass sich das Schwanken des Stativs fehlerhaft auf unsere Messungen auswirkte.
2. Mitten in unserer 2. Versuchsreihe setzte sich der hier fairerweise nicht namentlich genannte Fachlehrer zwecks einer Fotographie mitten auf den Tisch, an dem das Stativ festgeschraubt war. Es war ein deutliches Schwanken zu vermerken, was den Ausschlag sichtbar beeinflusste und unsere Messung damit verfälschte.
Wir haben versucht, all diesen Fehler mit mehreren Versuchsreihen
entgegenzuwirken und benutzten für die Graphik die Mittelwerte aller
Zeitmessungen.

Auswertungsfehler:

Die im Unterricht gegebenen Formeln gelten nur näherungsweise für kleine Winkel. Wir haben jedoch Winkel um die 20-30 Grad betrachtet.

Wir haben aus Gründen der Vereinfachung die Auslenkung aufgenommen. Diese ist jedoch nicht proportional zur Höhe. Um eine Frequenz aufnehmen zu können benötigt man aber diese Höhe. Wir hätten die aufgenommene Auslenkung mit Hilfe des Strahlensatzes in die tatsächliche Auslenkung umrechnen und somit über den Sinussatz die Höhe bestimmen können. Das haben wir nicht getan, also wurden die Werte mit einem sich immer ändernden Sinus aufgenommen, der besonders bei größeren Winkeln einen großen Fehler bewirkt.

Auswertung:

Bei der betrachteten Pendelbewegung treten unterschiedliche Arten von Reibung auf, sodass dem Oszillator mechanische Energie entzogen wird und sich die Amplitude verringert.

Wenn sich der Körper hin- und herbewegt tritt als Reibungswiderstand insbesondere ein Luftwiderstand in Erscheinung. Im Übrigen spielt noch ein Reibungswiderstand an der Aufhängung, sowie ein evtl. seitliches Ausscheren des Pendels aus der Bahn („nicht-lineare“ Pendelbahn) eine bedeutende Rolle.

Im Verlauf der Zeit nimmt die mechanische Energie des Systems ab, und die Energie wird in thermische Energie in Form von Reibungsverlusten umgewandelt.

Eine Untersuchung der Messwerte ergab, dass die Amplitude exponentiell verringert wird. Die Umlaufzeit bzw. die Frequenz bleiben jedoch - theoretisch gesehen - konstant.

Die gedämpfte Schwingung wird beschrieben durch die Funktion:

Wie gesagt spielt der Luftwiderstand bei dem vorliegenden Experiment eine zentrale Rolle, dieser ist proportional zum Quadrat der Geschwindigkeit.

Bei einer Halbierung der Geschwindigkeit verviertelt sich der Luftwiderstand: Die Verringerung der Amplitude erfolgt anfangs relativ schnell, dann immer langsamer.

Die genannten Zusammenhänge lassen sich auch mathematisch beschreiben, wobei diese allerdings nicht elementar aus wenigen Messwerten ableitbar sind.

Für eine gedämpfte Schwingung gilt: