Gruppe 4

Druckversion (pdf)		zurück
Bastian Inselmann, Nils Friedrich		Datum: 18.02.04
Physik LK 12/2 – Schwingungen und Wellen Fachlehrer Konrad
Thema:	Aufnahme einer Schwingung zur Bestimmung des Dämpfungsverhaltens über die Momentangeschwindigkeit im Nullpunkt.
Versuchsidee:	Im Vorfeld wurde zu diesem Experiment ein Hypothese aufgestellt, dass die Abnahme der Amplituden einer Schwingung einer exponentiellen Funktion genügt. Durch Vorherige Überlegungen wurde die lineare Abnahme der Amplituden ausgeschlossen. Um diese Hypothese zu Beweisen haben wir in unserer Gruppe die Schwingung eines Pendels über die Momentangeschwindigkeit im Nullpunkt. Diese haben wir über den Durchmesser des Pendels mit Hilfe eines Dunkelzeitmessers ermittelt. Aus der Geschwindigkeit kann dann wiederum über den Energieerhaltungssatz die Höhe des Ausschlags berechnet werden.
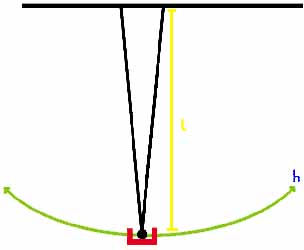
Aufbau:	Eine 3 cm breite Stahlkugel wird als Pendelkörper mit einer biflaren Aufhängung 1,7 Meter unter zwei festen Punkten (an der Zimmerdecke) befestigt, um eine Schwingung auf einer Ebene zu gewährleisten. Die Dunkelzeitmesser werden im Nullpunkt angebracht, wo die Kugel die höchste kinetische Energie besitzt. Einer der Dunkelzeitmesser misst die Anzahl der Schwingungen, der Andere misst die Zeit, die die Kugel benötigt um die Lichtschranke zu passieren.

Durchführung:	Die Kugel wird zum Schwingen gebracht und nach jeweils 10 Schwingungen wird mit Hilfe des Dunkelzeitmessers die Zeit gemessen, die die Kugel benötigt, um einmal die Lichtschranke zu passieren. Es wird danach, anhand der Zeit und des Durchmessers der Kugel, die jeweilige Geschwindigkeit des Pendels errechnet. Über den Energieerhaltungssatz ’WKin = WPot’ lässt sich aus der Geschwindigkeit mit einigem Umformen die theoretisch erreichte Höhe errechnen (sie wird bei andauernder Dämpfung zwar nie direkt erreicht, ist aber trotzdem Ausreichend):



Messwerte:



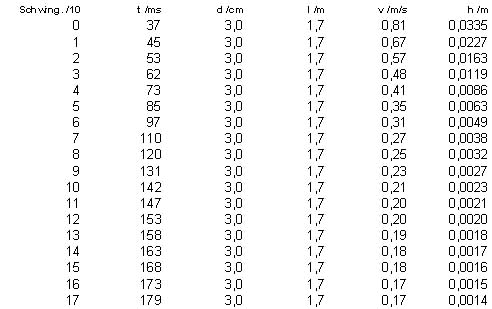Fehlerbetrachtung:	Der größte Fehlereinfluss wird wohl die Ungenauigkeit des Dunkelzeitmessgeräts sein. Es hat einen (angenommenen) Grundfehler von 1,5%. Darüber hinaus ist die Anzeige auf die Millisekunde genau unzureichend, das dadurch ein zusätzlicher Fehler von einer Millisekunde durch Rundungen entstehen kann. Ablesefehler können komplett ausgeschlossen werden. Weitere Fehleinflüsse sind durch die hohe Fadenlänge und die bifilare Aufhängung minimiert. Beschränkt auf Messfehler ließe sich somit wie folgt errechnen: Beim ersten Wert ist ein maximaler Fehler von 1 ms + 0,5 ms, also von 4,2% möglich. Trotzdem sind 1,5 ms Verschiebung nicht wirklich kritisch, da sehr große Abstände zu den darauffolgenden Werten vorhanden sind. Der Fehler könnte 19% des Abstandes ausmachen. Beim letzten Wert dagegen wären es 1 ms + 2,7 ms, also nur von 2%. Doch diese 3,7 ms sind fast zwei Drittel des Abstandes zum nächsten Wert, somit sind der Fehleinflüsse bei geringeren Geschwindigkeiten um einiges größer als bei der Geschwindigkeit am Anfang des Experiments.
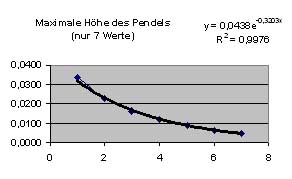
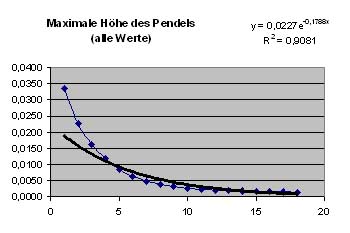
Auswertung:	Im Ansatz – vor allem bei der ausschließlichen Betrachtung der ersten Werte – wurde die Theorie einer exponentiellen Abnahme bestätigt. Es lässt sich klar eine Halbwertszeit erkennen und auch eine passende Funktion finden. Wenn mal allerdings auf alle 18 Werte zurückgreift, so lässt sich keine Halbwertszeit bestimmen oder Kurve zeichnen – die Daten sind durch den zu großen Fehler unbrauchbar! Generell ist dieses Experiment durchaus brauchbar zur Bestimmung des Dämpfungsverhaltens bei Schwingungen, allerdings lässt die finale Genauigkeit noch zu wünschen übrig. Bei einer Wiederholung des Experimentes sollte vor allem an den Messungen gearbeitet werden. Eine höhere Anfangsgeschwindigkeit und ein genaueres Messinstrument würden die Abweichungen von der exponentiellen Abnahme minimieren.