Lineare Funktionen
|
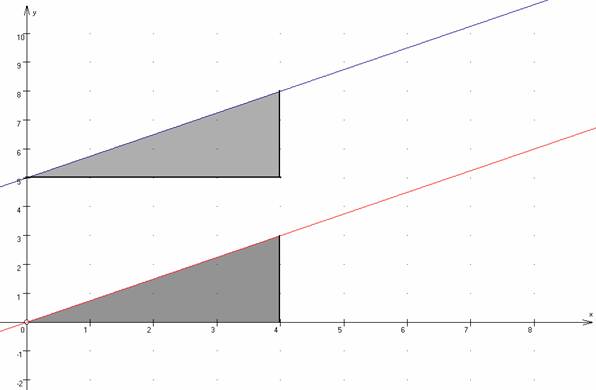
g(x) = ¾ × x + 5
f(x) = ¾ × x
|
Man erhält den Graphen der Funktion g mit der Gleichung
y = f(x) = mx + b , Geradengleichung
indem man die Ursprungsgerade mit y = mx parallel zur y-Achse um b verschiebt.
Definition: Eine Funktion mit einer Funktionsgleichung der Form y = f(x) = mx + b,
x, m, b Î Q heißt lineare Funktion.
Bestimmung
der Geradengleichung
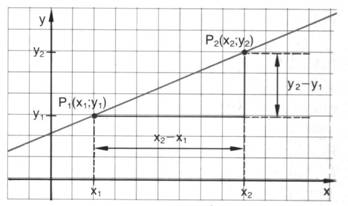
P1 und P2 seien zwei Punkte der Gerade.
Die Differenzen der y-Koordinaten ( y1 – y2 )
und x-Koordinaten ( x1 – x2 ) ,
wobei x1 ≠ x2 , bestimmen die Seitenlängen im Steigungsdreieck.
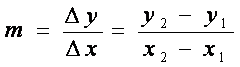
Das Einsetzen von m und einem Koordinatenpaar in die Geradengleichung liefert b.
y1 = m×x1 + b ® b = y1 – mx1
